Thematisches, allgemein und speziell

Bezugssystem und Definitionen

Es werden hier ausschließlich Motivservietten ( und Motivtaschentücher ) betrachtet.
Für die weiteren Betrachtungen werden nun die folgenden Vereinbarungen getroffen:

•  Drei wesentliche Begriffe 
  • Motiv      –  Dasjenige, was abgebildet wird
  • Bild        –  Das Ergebnis des Abbildens
  • Bereich  –  Die Stelle, wo sich das Bild befindet
•  Bezugssystem 
  • Die Serviette wird in der sog. „Kanten–Lage” betrachtet, bei welcher die Kanten der Serviette waagerecht bzw. senkrecht verlaufen.
  • Die OW–Achse und die NS–Achse zerlegen der Serviette in vier gleich große Quadrate, die im weiteren als  SW–, SO–, NO–, NW–Bereich  bezeichnet werden; siehe Abb. 1.
  • Jedes dieser vier Quadrate könnte als SW–Bereich gewählt werden. Das Bild im SW–Bereich sollte sich jedoch immer in der  „natürlichen Lage”  befinden, also z.B. ein Baum mit der Krone nach oben. Für dieses Bild im SW–Bereich wird immer das Symbol gemäß Abb. 2 verwendet.
  • Befindet sich allerdings der Name oder ein Logo des Herstellers oder des Designers auf dem Objekt, dann sollte dieser / dieses möglichst auch im SW–Bereich liegen. Dies lässt sich allerdings nicht immer realisieren; in einem solchen Fall hat die  „natürliche Lage” des Bildes im SW–Bereich Priorität.
  • Bei nur 1 Bild gibt es 44=256 Möglichkeiten seiner Anordnung. Befindet sich das Bild im SW–Bereich jedoch immer in der „natürlichen Lage”, dann reduziert sich die Anzahl auf 43=64 Möglichkeiten, von denen die meisten allerdings nicht von Interesse sind. Bei 2 Bildern ist die Mannigfaltigkeit der Anordnung noch sehr viel größer, und soll daher nicht weiter erörtert werden.
    
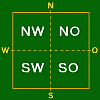
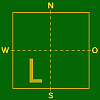
    Abbildung 1 Abbildung 2

•  Verwendete Symbole für die vier Bilder B.1 bis B.4 
  
  • B.1    B.1 horiz. gesp.    B.1 vertik. gesp.    B.1 horiz. u. vertik. gesp.
  • B.2    B.2 horiz. gesp.    B.2 vertik. gesp.    B.2 horiz. u. vertik. gesp.
  • B.3    B.3 horiz. gesp.    B.3 vertik. gesp.    B.3 horiz. u. vertik. gesp.
  • B.4    B.4 horiz. gesp.    B.4 vertik. gesp.    B.4 horiz. u. vertik. gesp. ( Bei vertikaler Spiegelung sind die Motive „kopfstehend” )

•  Drei fiktive Bildebenen 
  • Für die weiteren Betrachtungen ist es nützlich, drei übereinanderliegende, fiktive Bildebenen einzuführen. Diese sind bis auf die darin enthaltenen Bildelemente durchsichtig, und können gleiche oder auch unterschiedliche Symmetrieeigenschaften aufweisen.
  • Motiv–Ebene
    • Sie enthält die eigentlich interessierenden Bilder.
    • Sie kann in jedem der o.g. vier Teilbereiche das gleiche Bild oder aber unterschiedliche Bilder enthalten, wobei diese sowohl ungespiegelt als auch ein– oder mehrfach gespiegelt auftreten können.
  • Hintergrund–Ebene
    • Sie enthält kleinformatige Bildelemente oder ist leer.
  • Rand–Ebene
    • Sie enthält kleinformatige Bildelemente oder ist leer.
    • Ihre Bildelemente umrahmen die Gesamtheit aller Bildelemente der Motiv–Ebene und der Hintergrund–Ebene.
    • Ihre Bildelemente können jeden der o.g. vier Teilbereiche zusätzlich umrahmen.

•  Einordnung der Servietten hinsichtlich ihrer geometrischen Eigenschften 
  
  • Von allen unwesentlichen Bildelementen und eventuellen Aufdrucken ( Logo, Name usw. ) wird angenommen, dass sie in der Hintergrund–
    bzw. in der Rand–Ebene liegen.
  • Bei der Einordnung der Servietten werden die geometrischen Eigenschaften dieser beiden Ebenen vernachlässigt.
  • Damit sind für die Einordnung der Servietten nur die geometrischen Eigenschaften der Motiv–Ebene von Bedeutung.
  • Natürlich ist dieses Vorgehen relativ willkürlich; aber hierdurch kommt das für die Einordnung Wesentliche erst klar zum Vorschein.

Geometrische Eigenschaften

Bei Servietten mit 1 Bild bzw. mit 2 Bildern kann die Serviette durch bestimmte Operationen an diesen Bildern vollständig mit ihnen ausgefüllt werden; bei Servietten mit 4 Bildern ist dies nicht mehr möglich.
Abhängig von der Art der ausgeführten Operationen entstehen so unterschiedliche Gesamtbilder vom „Verschiebungs–Typ”, vom „Spiegelungs–Typ” oder aber vom „Misch–Typ”; außerdem sind noch „Sonder–Typen” möglich, die sich in die 3 erstgenannten Gruppen nicht einordnen lassen. Als Operationen sind nur Verschiebungen und Spiegelungen des Bildes / der Bilder zulässig.

•  Gesamtbilder vom Verschiebungs–Typ 
  • Gesamtbilder als sog. „Tapeten”
    • Zulässige Operationen: Verschiebungen in OW–Richtung
      und / oder in NS–Richtung.
    • Man kann diese Art von Gesamtbildern mit einer  Tapete 
      vergleichen. Dabei gibt es nur ein einziges Bild, das dem  Muster  der Tapete entspricht.
    • Gesamtbilder dieses Typs haben im allg. weder Spiegelungs– noch Symmetrieeigenschaften; sie können im allg. auch durch keine der o.g. Operationen in sich selbst überführt werden.
    • Ausnahmen davon sind Gesamtbilder vom „Misch–Typ”, die in Tabelle 2 aufgeführt sind.
  • Tapeten im engeren Sinne
    
    • Eine  Tapete im engeren Sinne  liegt dann vor, wenn mindestens eine der beiden Abmessungen des Musters ( Breite b, Höhe h ) einen Wert zwischen 0 und K oder zwischen K und 2K aufweist. Für den Wert 0 liegt kein Muster vor; die Fälle für die Werte K und 2K findet man in Tabelle 3.
    • Tabelle 1  –  Tapeten im engeren Sinne ohne Versatz.
      Es werden die folgenden Bezeichnungen verwendet:
       b  – Breite des Musters;  h  – Höhe des Musters
       K  – halbe Kantenlänge der Serviette

      Maße	0 < h < K	h = K	K < h < 2K
      0 < b < K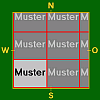
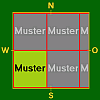
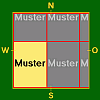
      b = K	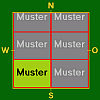	siehe Tabelle 3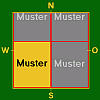
      K < b < 2K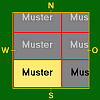

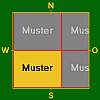
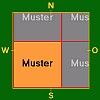
    • Die Zeile mit  b = 2K  und die Spalte mit  h = 2K  wurde in obige Tabelle nicht mit aufgenommen. Sie enthalten einerseits Fälle, die bisher nicht aufgetreten sind und wohl auch nicht auftreten werden, und sie enthalten andererseits einige Sonderfälle, die in Tabelle 3 erläutert werden.
    • Zusätzlich kann ein sog.  Versatz  auftreten ( ähnlich wie bei den richtigen Tapeten ).
    • Als Beispiel für  Tapeten mit Versatz  wird der Fall  b < K,  h < K  an Hand folgender Skizzen gezeigt; auf die Darstellung weiterer Fälle mit Versatz wird verzichtet:
               
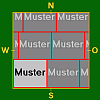
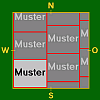
      ohne Versatz mit OW–Versatz mit NS–Versatz

•  Gesamtbilder vom Misch–Typ 
  • Zulässige Operationen: Verschiebung entweder in OW–Richtung oder in NS–Richtung, einfache Spiegelung entweder um die OW–Achse oder um die NS–Achse.
  • Gesamtbilder vom Misch–Typ können nur bei 1 Bild auftreten.
  • Ein Gesamtbild vom Misch–Typ hat stets bestimmte Symmetrieeigenschften.
  • Die Gesamtbilder vom Misch–Typ sind in Tabelle 2 mit enthalten.

•  Gesamtbilder vom Spiegelungs–Typ 
  • Zulässige Operationen: einfache und mehrfache Spiegelungen von einem Bild bzw. von zwei nebeneinanderliegenden Bildern um die OW–Achse
    und / oder um die NS–Achse.
  • Gesamtbilder vom Spiegelungs–Typ haben stets bestimmte Symmetrie– eigenschaften.
  • Zentralsymmetrie
    • Dieser Fall kann bei 1 Bild und bei 2 Bildern auftreten.
    • Spiegeln des Gesamtbildes an beiden Achsen ( OW–Achse
      und NS–Achse ) überführt das Gesamtbild in sich selbst.
    • Diese Spiegelung entspricht einer Drehung um 180°.
    • Bei 1 Bild sind die Gesamtbilder z.T. vom Spiegelungs–Typ und z.T. vom Misch–Typ ( Sonderfälle von Tapeten in OW–Richtung
      bzw. in NS–Richtung ).
    • Bei 2 Bildern existiert nur der Spiegelungs–Typ.
  • Axialsymmetrie nur bezüglich OW–Achse
    • Dieser Fall kann bei 1 Bild und bei 2 Bildern auftreten.
    • Spiegeln des Gesamtbildes an der OW–Achse überführt das
      Gesamtbild in sich selbst.
    • Das Gesamtbild kann durch Drehung NICHT in sich selbst überführt werden.
    • Bei 1 Bild sind die Gesamtbilder z.T. vom Spiegelungs–Typ und z.T. vom Misch–Typ ( Sonderfall einer Tapete in OW–Richtung ).
    • Bei 2 Bildern existiert nur der Spiegelungs–Typ.
  • Axialsymmetrie nur bezüglich NS–Achse
    • Dieser Fall kann bei 1 Bild und bei 2 Bildern auftreten.
    • Spiegeln des Gesamtbildes an der NS–Achse überführt das
      Gesamtbild in sich selbst.
    • Das Gesamtbild kann durch Drehung NICHT in sich selbst überführt werden.
    • Bei 1 Bild sind die Gesamtbilder z.T. vom Spiegelungs–Typ und z.T. vom Misch–Typ ( Sonderfall einer Tapete in NS–Richtung ).
    • Bei 2 Bildern existiert nur der Spiegelungs–Typ.
  • Axialsymmetrie bezüglich OW–Achse und NS–Achse
    
    • Dieser Fall kann nur bei 1 Bild auftreten.
    • Spiegeln des Gesamtbildes an mindestens einer Achse
      ( OW–Achse oder NS–Achse ) überführt dieses Bild in sich selbst.
    • Jede dieser drei möglichen Spiegelungen entspricht einer
      Drehung um 180°.
    • Es existiert nur ein Gesamtbild vom Spiegelungs–Typ.
  • Tabelle 2  –  Spiegelungs– und Misch–Typen bei 1 Bild bzw. bei 2 Bildern

    Eigensch.	1 Bild	2 Bilder
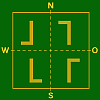
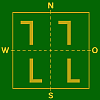
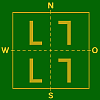
    Zentral–   symmetrie	Spiegelungs–Typ Misch–Typen	Spiegelungs–Typ 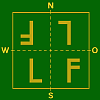und weitere bisher nicht aufgetretene Fälle
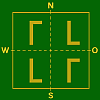
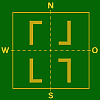
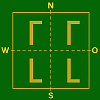
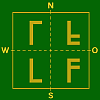
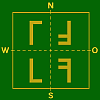
    Axial–   symmetrie   nur   bezüglich   OW–Achse	Spiegelungs–Typen Misch–Typ	Spiegelungs–Typen und weitere bisher nicht aufgetretene Fälle
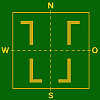
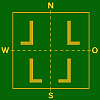
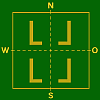
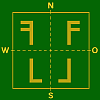
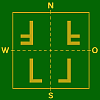
    Axial–   symmetrie   nur   bezüglich   NS–Achse	Spiegelungs–Typen Misch–Typ	Spiegelungs–Typen und weitere bisher nicht aufgetretene Fälle
    Axial–   symmetrie   bezüglich   OW–Achse   und   NS–Achse	Spiegelungs–Typ	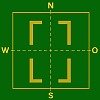Fall existiert nicht

   

•  Sonderfälle des Verschiebungs–Typs und weitere Sonder–Typen ( ohne Symmetrie ) 
  
  • Gesamtbilder vom Verschiebungs–Typ:
      a )  Das Muster nimmt ein Viertel der Serviette ein.
      b )  Das Muster nimmt die Hälfte der Serviette ein ( vertikal ).
      c )  Das Muster nimmt die Hälfte der Serviette ein ( horizontal ).
      d )  Das Muster nimmt die gesamte Serviette ein; es liegt ein „Vollbild” vor.
  • Gesamtbilder als Sonder–Typ mit 4 Teilbildern:
      e )  Es liegt der Fall „Vier eigenständige Bilder” vor; hier sind nur die
            bisher aufgetretenen Fälle dargestellt.
    
  • Tabelle 3 a

    Eigensch.	1 Bild	2 Bilder
    a)  b = h = K	Verschiebung längs OW–Achse und NS–Achse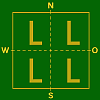	Fall existiert nicht
    b)  b = K   und   h = 2K	Verschiebung längs OW–Achse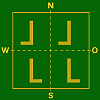	Verschiebung längs OW–Achse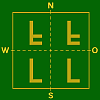
    c)  b = 2K   und   h = K	Verschiebung längs NS–Achse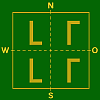	Verschiebung längs NS–Achse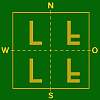

  • Tabelle 3 b

    Eigensch.	4 Bilder
    d)  b = h = 2K	4 Teilbilder ohne eigenständige Bedeutung ( Vollbild )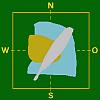
    e)  Sonder–   Typen	4 eigenständige Bilder 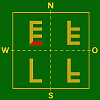Bilder unten und oben: „natürliche Lage”	4 eigenständige Bilder 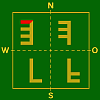Bilder unten: „natürliche Lage”, Bilder oben: „kopfstehend”

  • In den Tabellen 2 und 3 sind die folgenden Sonderfälle von Tapeten nicht enthalten, da sie bei den bisher eingearbeiteten Servietten noch nicht aufgetreten sind, und vermutlich auch nicht auftreten werden:
    • Tapete in NS–Richtung, bei der sich das Muster über die
      gesamte Breite der Serviette erstreckt:
      b = 2K  und  0 < h < K         sowie       b = 2K  und  K < h < 2K
    • Tapete in OW–Richtung, bei der sich das Muster über die
      gesamte Höhe der Serviette erstreckt:
      0 < b < K    und  h = 2K       sowie       K < b < 2K  und  h = 2K

Ergänzungen zu Servietten in „Eck–Lage”

Die bisherigen Darstellungen beziehen sich ausschließlich auf Servietten in der Kanten–Lage. Bei manchen Servietten erscheinen die Bilder jedoch erst dann in natürlicher Lage, wenn sich die Serviette in der sog. Eck–Lage befindet.

•  Eck–Lage 
  • Die Kanten der Serviette verlaufen unter 45° bzw. 135°, und die o.g. vier Bereiche gemäß Abb. 1 befinden sich nun ebenfalls in Eck–Lage ( siehe Abb. 3 ).
  • Ein Name oder ein Logo des Herstellers sollte sich wieder möglichst im SW–Bereich, nun unten liegend, befinden.
  • Betrachtet man eine solche Serviette in Eck–Lage statt in Kanten–Lage, dann erscheinen das Bild / die Bilder um einen Winkel von 45° gedreht.

•  Eigenschaften 
  • Die folgende Abb. 3 zeigt als Beispiele zwei typische Fälle ( für 1 Bild ):
  • 
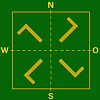
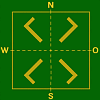
  • Kanten–Lage Eck–Lage Kanten–Lage Eck–Lage
  • In Eck–Lage können wieder alle für die Kanten–Lage beschriebenen Typen auftreten, wobei nun zusätzlich die Symmetrieeigneschaften bezüglich der beiden Diagonalen eine Rolle spielen.
  • Da jedoch bisher nur einige Servietten in Eck–Lage vorliegen, wird auf eine ausführliche Darstellung der möglichen Fälle verzichtet.

Hier geht es zum Inhaltsverzeichnis des Albums der  Papierservietten mit Pilzmotiven.